Jump to
Stay tuned for
more insights
Follow us on
Manipulating Numeric Parameters
Numeric parameters are control variables that drive almost every web application. As ethical hackers, modifying these numbers is one of the most basic but also most important tasks we perform. During a vulnerability assessment, parameters are modified thousands of times in different ways to test the security controls of a web application. Over the years, one of these ways has remained the most common and prevalent way to bypass access restrictions of an application: incrementing or decrementing numbers. One of the most common places we see parameters we wish to modify are in simple GET requests:
http://example.com/editpreferences.aspx?userid=1000234
http://example.com/user/1000234/editpreferences</pre>Because this type of testing is such a repetitive task, we will talk for a moment on efficiency. While we normally use a proxy to intercept, modify, and send parameters to the server, we can modify these faster and easier than that. Because we encounter examples of this on almost every assessment, saving one or two seconds per test case is a valuable benefit. For this we turn to a small Firefox utility called URL Flipper. With this small add-on we can use Ctrl-Shift-Up or Ctrl-Shift-Down hotkeys to quickly “flip” through many parameters as well as view the output rendered in the browser.
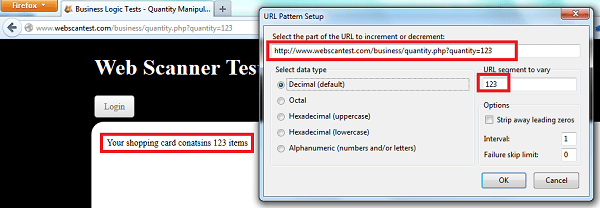
As shown above, we used this to quickly flip through 10 or 20 “quantity” values. While in this example is useful for relatively small increments, it won’t serve us well for all test cases. Incrementing numbers may often require us to search a far greater span of numbers than is feasible by this method. For very large groups of numbers where we may be searching for account numbers, profile IDs, etc, we can use a more powerful automated assistant. Burp intruder provides one of the most powerful scripted search and replace functions available to ethical hackers.
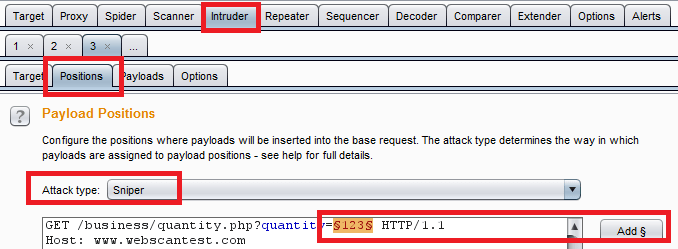
Here we use Burp intruder to specify a position (the ‘quantity’ parameter), and we will then set a type of payload. Below shows the payload configuration where we specify ‘Numbers’ as the payload type, and configure the range of values we wish to search for.
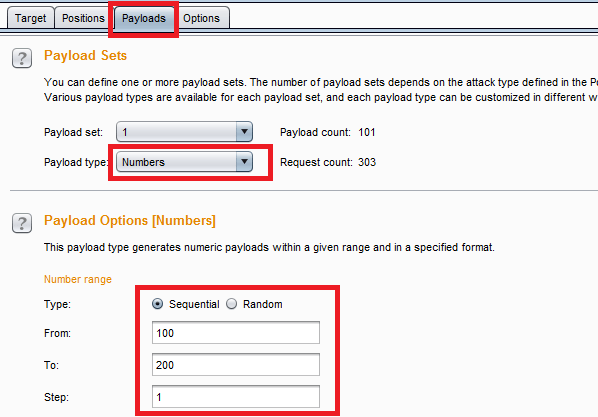
This is an extremely powerful way for us to search a larger set of parameters. But as we scan a larger range, making sense of the results becomes increasingly difficult. We don’t have the time to manually examine 200 or even 2000 results, so we will examine differentiation. Sorting by response length is an easy way to look for pages that might be different than the others. While this example does not show us a result set where we can sort for anything of value, sorting will be required in most real life testing. Burp also has a filter where we can search by string, regex, or response code.
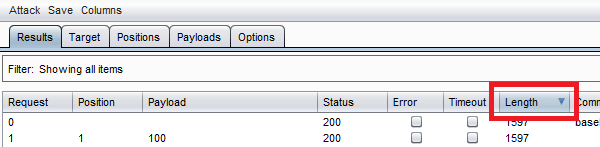
There are many situations where application arithmetic can be abused to bypass business logic. One classic financial example is using fractions of cents. Imagine we have a money transfer function that transfers money from one account to another, how can we be sure the application properly handles all decimal values? What if an application ignored the values past the second decimal, but the database still honored the transaction? To test this we will replay the function several hundred times and compare the amounts in both accounts to what they were previously. Below shows an example of a request where such an attack might be feasible:
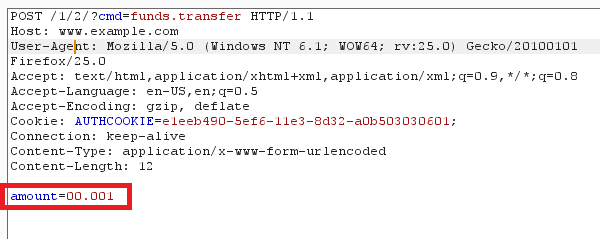
We can feed this again to Intruder to replay this. Instead of ‘numbers’ as a payload we will use ‘null payloads’:

These techniques can be applied to real attacks on the vast majority of web applications. And now that we have the technical methods covered, we can focus again on the logical attacks. When reviewing an application, we must constantly be aware of the function we are performing, and what control variables we possess. Are we viewing an order? Do we control an order ID parameter? Are we transferring money? Do we control the source account ID? This is what we must determine for every secure function within an application. Another way we can sometimes subvert application arithmetic is by attempting to overflow stored integer values. We must remember that not all systems may treat integers the same. A front end Java application may handle the number 2,147,483,648 without any problem, while this same number may overflow a 32 bit signed integer on a backend system; this number may now be represented as a negative value. In summary, below are four key areas to look for when the user controls numeric values used by the application:
- Bypassing permissions – changing parameters for order IDs, account IDs, profile IDs, etc.
- Using negative values – causing a subtraction instead of addition.
- Using decimal values – causing unexpected calculations of orders or transactions.
- Using large values – overflowing or underflowing variables will always cause unexpected (and unintended) results.
While this is not a complete checklist for testing these parameters, it is something testers should keep in mind. Every application is unique and has a highly subjective threat model. In ethical hacking assessments, performing a thorough analysis of the functionality and then developing custom attacks must always be the first priority.
